Fundamentals Of Quantum Information (Quantum Teleportation ) - Innsbruck University | Anton Zeilinger

The fact that information is physical means that the laws of quantum mechanics can be used to process and transmit it in ways that are not possible with existing systems.

Ever since its invention in the 1920s, quantum physics has given rise to countless discussions about its meaning and about how to interpret the theory correctly. These discussions focus on issues like the Einstein-Podolsky-Rosen paradox, quantum non-locality and the role of measurement in quantum physics. In recent years, however, research into the very foundations of quantum mechanics has also led to a new field - quantum information technology. The use of quantum physics could revolutionize the way we communicate and process information.

The important new observation is that information is not independent of the physical laws used to store and processes it (see Landauer in further reading). Although modern computers rely on quantum mechanics to operate, the information itself is still encoded classically. A new approach is to treat information as a quantum concept and to ask what new insights can be gained by encoding this information in individual quantum systems. In other words, what happens when both the transmission and processing of information are governed by quantum laws?

The elementary quantity of information is the bit, which can take on one of two values - usually "0" and "1". Therefore, any physical realization of a bit needs a system with two well defined states, for example a switch where off represents "0" and on represents "1". A bit can also be represented by, for example, a certain voltage level in a logical circuit, a pit in a compact disc, a pulse of light in a glass fibre or the magnetization on a magnetic tape. In classical systems it is desirable to have the two states separated by a large energy barrier so that the value of the bit cannot change spontaneously.

Two-state systems are also used to encode information in quantum systems and it is traditional to call the two quantum states 0ñ and 1ñ. The really novel feature of quantum information technology is that a quantum system can be in a superposition of different states. In a sense, the quantum bit can be in both the 0ñ state and the 1ñ state at the same time. This new feature has no parallel in classical information theory and in 1995 Ben Schuhmacher of Kenyon College in the US coined the word "qubit" to describe a quantum bit.

A well known example of quantum superposition is the double-slit experiment in which a beam of particles passes through a double slit and forms a wave-like interference pattern on a screen on the far side. The essential feature of quantum interference is that an interference pattern can be formed when there is only one particle in the apparatus at any one time. A necessary condition for quantum interference is that the experiment must be performed in such a way that there is no way of knowing, not even in principle, which of the Quantum interference can be explained by saying that the particle is in a superposition of the two experimental paths: passage through the upper slitñ and passage through the lower slitñ. Similarly a quantum bit can be in a superposition of 0ñ and 1ñ. Experiments in quantum information processing tend to use interferometers rather than double slits but the principle is the same (see right). So far single-particle quantum interference has been observed with photons, electrons, neutrons and atoms.

Beyond the bit

Any quantum mechanical system can be used as a qubit providing that it is possible to define one of its states as 0ñ and another as 1ñ. From a practical point of view it is useful to have states that are clearly distinguishable. Furthermore, it is desirable to have states that have reasonably long lifetimes (on the scale of the experiment) so that the quantum information is not lost to the environment through decoherence. Photons, electrons, atoms, quantum dots and so on can all be used as qubits. It is also possible to use both internal states, such as the energy levels in an atom, and external states, such as the direction of propagation of a particle, as qubits (see table).

The fact that quantum uncertainty comes into play in quantum information might seem to imply a loss of information. However, superposition is actually an asset, as can be seen when we consider systems of more than one qubit. What happens if we try to encode two bits of information onto two quantum particles? The straightforward approach would be to code one bit of information onto each qubit separately. This leads to four possibilities - 0ñ₁ 0ñ₂ 0ñ₁ 1ñ₂ 1ñ₁ 0ñ₂ and 1ñ₁ 1ñ₂ - where 0ñ₁ 1ñ₂ describes the situation where the first qubit has the value "0" and second qubit has the value "1", and so on. This approach corresponds exactly to a classical coding scheme in which these four possibilities would represent "00", "01", "10" and "11".

However, quantum mechanics offers a completely different way of encoding information onto two qubits. In principle it is possible to construct any superposition of the four states described above. A widely used choice of superpositions is the so-called Bell states. A key feature of these states is that they are "entangled" (see box). Entanglement describes correlations between quantum systems that are much stronger than any classical correlations.

As in classical coding, four different possibilities can be represented by the four Bell states, so the total amount of information that can be encoded onto the two qubits is still two bits. But now the information is encoded in such a way that neither of the two qubits carries any well defined information on its own: all of the information is encoded in their joint properties. Such entanglement is one of the really counterintuitive features of quantum mechanics and leads to most of the paradoxes and other mysteries of quantum mechanics (see Bell's inequality and quantum non-locality).

It is evident that if we wish to encode more bits onto quantum systems, we have to use more qubits. This results in entanglements in higher dimensions, for example the so-called Greenberger-Horne-Zeilinger (GHZ) states, which are entangled superpositions of three qubits (see further reading). In the state 1/2( 000ñ + 111ñ), for instance, all three qubits are either "0" or "1" but none of the qubits has a well defined value on its own. Measurement of any one qubit will immediately result in the other two qubits attaining the same value.

Although it was shown that GHZ states lead to violent contradictions between a local realistic view of the world and quantum mechanics, it recently turned out that such states are significant in many quantum-information and quantum-computation schemes. For example, if we consider 000 and 111 to be the binary representations of "0" and "7", respectively, the GHZ state simply represents the coherent superposition (1/Ö2)( "0"ñ + "7"ñ). If a linear quantum computer has such a state as its input, it will process the superposition such that its output will be the superposition of the results for each input. This is what leads to the potentially massive parallelism of quantum computers.

It is evident that the basis chosen for encoding the quantum information, and the states chosen to represent 0ñ and 1ñ, are both arbitrary. For example, let us assume that we have chosen polarization measured in a given direction as our basis, and that we have agreed to identify the horizontal polarization of a photon with "0" and its vertical polarization with "1". However, we could equally well rotate the plane in which we measure the polarization by 45º. The states in this new "conjugate" basis, 0´ñ and 1´ñ, are related to the previous states by a 45º rotation in Hilbert space

0´ñ = (1/Ö2)( 0ñ + 1ñ)

1´ñ = (1/Ö2)( 0ñ - 1ñ)

This rotation is known in information science as a Hadamard transformation. When spin is used to encode information in an experiment we can change the basis by a simple polarization rotation; when the directions of propagation are used, a beam splitter will suffice. It is important to note that conjugate bases cannot be used at the same time in an experiment, although the possibility of switching between various bases during an experiment - most notably between conjugate bases - is the foundation of the single-photon method of quantum cryptography.

Quantum dense coding

Entangled states permit a completely new way of encoding information, as first suggested by Charles Bennett of the IBM Research Division in Yorktown Heights, New York, and Stephen Wiesner of Brookline, Massachusetts, in 1992. Consider the four Bell states: it is clear that one can switch from any one of the four states to any other one by simply performing an operation on just one of the two qubits. For example, one can switch from Y⁺ñ to Y^-ñ by simply applying a phase shift to the second qubit when it is "0" (i.e. 0ñ ® - 0ñ, 1ñ ® 1ñ). The state f⁺ñ can be obtained by "flipping" the second qubit, while the state f^-ñ can be obtained by the combination of a phase shift and flipping.

All three of the operations are unitary and they do not change the total probability of finding the system in the states 0ñ and 1ñ. In working with Bell states it is common to refer to four unitary operations: the phase shift, the bit flip, the combined phase-shift/bit-flip, and the identity operator, which does not change the state on which it operates. All four operations are relatively easy to perform in experiments with photons, atoms and ions.two slits the particle passed through on its way to the screen.

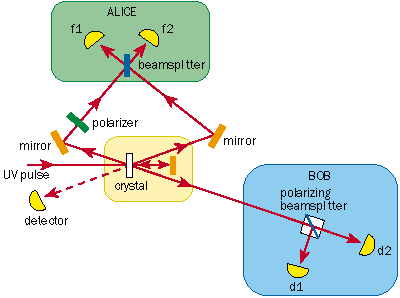
To understand what this means, imagine that Bob wants to send some information to Alice. (The characters in quantum information technology are always called Alice and Bob.) Entanglement means that, in theory, Bob can send two bits of information to Alice using just one photon, providing that Alice has access to both qubits and is able to determine which of the four Bell states they are in (see left).

This scheme has been put into practice by my group in Innsbruck using polarization-entangled photons (see Mattle et al . in further reading). The experiment relies on the process of spontaneous parametric down-conversion in a crystal to produce entangled states of very high quality and intensity. The nonlinear properties of the crystal convert a single ultraviolet photon into a pair of infrared photons with entangled polarizations.

The experiment used quarter- and half-wave polarization plates (plates that shift the phase between the two polarization states of a photon by l/4 and l/2, respectively) to make the unitary transformations between the Bell states. In fact it is possible to identify only the Y⁺ñ and Y^-ñ states uniquely using linear elements such as wave plates and mirrors. However, by being able to discriminate between three different possibilities - Y⁺ñ, Y^-ñ and f^±ñ - Bob could send one "trit" of information with just one photon, even though the photon had only two distinguishable polarization states. It has been shown that a nonlinear quantum gate will be needed to distinguish between all four Bell states. Such a gate would depend on a nonlinear interaction between the two photons and various theoretical and experimental groups are working on this challenge.

Quantum teleportation

Quantum dense coding was the first experimental demonstration of the basic concepts of quantum communication. An even more interesting example is quantum teleportation.

Suppose Alice has an object that she wants Bob to have. Besides sending the object itself, she could, at least in classical physics, scan all of the information contained in the object and transmit that information to Bob who, with suitable technology, could then reconstitute the object. Unfortunately, such a strategy is not possible because quantum mechanics prohibits complete knowledge of the state of any object.

There is, fortunately, another strategy that will work. What we have to do is to guarantee that Bob's object has the same properties as Alice's original. And most importantly, we do not need to know the properties of the original. In 1993 Bennett and co-workers in Canada, France, Israel and the US showed that quantum entanglement provides a natural solution for the problem (see further reading).

 

In this scheme Alice wants to teleport an unknown quantum state Yñ to Bob (see left). They both agree to share an entangled pair of qubits, known as the ancillary pair. Alice then performs a joint Bell-state measurement on the teleportee (the photon she wants to teleport) and one of the ancillary photons, and randomly obtains one of the four possible Bell results. This measurement projects the other ancillary photon into a quantum state uniquely related to the original. Alice then transmits the result of her measurement to Bob classically, and he performs one of the four unitary operations to obtain the original state and complete the teleportation.

It is essential to understand that the Bell-state measurement performed by Alice projects the teleportee qubit and her ancillary photon into a state that does not contain any information about the initial state of the teleportee. In fact, the measurement projects the two particles into a state where only relative information between the two qubits is defined and known. No information whatsoever is revealed about Yñ. Similarly, the initial preparation of the ancillary photons in an entangled state provides only a statement of their relative properties. However, there is a very clear relation between the ancillary photon sent to Bob and the teleportee photon. In fact, Bob's photon is in a state that is related to Alice's original photon by a simple unitary transformation.

Consider a simple case. If Alice's Bell-state measurement results in exactly the same state as that used to prepare the ancillary photons (which will happen one time in four), Bob's ancillary photon immediately turns into the same state as Yñ. Since Bob has to do nothing to his photon to obtain Yñ, it might seem as if information has been transferred instantly - which would violate special relativity. However, although Bob's photon does collapse into the state Yñ when Alice makes her measurement, Bob does not know that he has to do nothing until Alice tells him. And since Alice's message can only arrive at the speed of light, relativity remains intact.

In the other three possible cases, Bob has to perform a unitary operation on his particle to obtain the original state, Yñ. It is important to note, however, that this operation does not depend at all on any properties of Yñ.

The main challenge in our experiment was to perform a Bell-state measurement on two particles that were generated independent of each other (see Bouwmeester et al. in further reading). Since a Bell-state measurement probes the collective or relative properties of two quantum particles, it is essential that the particles "forget" any information about where they were generated. To achieve this we must perform the experiment in such a way that we are unable, even in principle, to gain any path information. We do this by directing the two photons - the teleportee and Alice's ancillary - through a semitransparent beam splitter from opposite sides (see right). We then ask a simple question: if the two particles are incident at the same time, how will they be distributed between the two output directions?

Since photons were used in the experiment, one might naively have expected that both photons would emerge in the same output beam. This feature, called "bunching", is well known for bosons (particles with integer spin such as photons) and was demonstrated with optical beam splitters for the first time in 1987 by Leonard Mandel's group at the University of Rochester in the US. Surprisingly, perhaps, bunching only happens for three of the Bell states. In contrast, for the Y^-ñ state , the photons always leave in different beams. In other words, the photons "anti-bunch" and behave as if they were fermions. This is a direct consequence of interference.

This means that for the Y^-ñ state we have no way of knowing which way the photons reached the detectors: both photons could have been transmitted by the beam splitter, or both could have been reflected. By adding various polarizers it is also possible to identify photons in the Y⁺ñ state. As with dense coding, however, quantum gates will be needed to make the experiment work with the f⁺ñ and f^-ñ states.

In the actual experiment the teleportee photon was also made using parametric down-conversion (see left). This provides an additional photon that can be used as a trigger informing us that the teleportee photon is "ready". The experiment itself involved preparing the teleportee photon in various different polarization states - horizontal, vertical, +45º, -45º and right-hand circular - and proving that Bob's photon actually acquired the state into which the teleportee photon was prepared. The teleportation distance was about 1 metre. Since the experiment was set up to identify only the Y^-ñ state, the maximum success rate for teleportation was, in theory, 25%, and the measured success rate was much lower.

A related experiment was recently performed at the University of Rome La Sapienza (see Boschi et al . in further reading) using only one entangled pair of photons. In this experiment Alice was able to prepare Bob's particle at a distance, again to within an unitary transformation. By essentially performing a Bell-state measurement on two properties of the same photon, the Rome group was able to distinguish between all four Bell states simultaneously.

The entanglement of photons over distances as great as 10 km has now been demonstrated at the University of Geneva, so teleportation is expected to work over similar distances. The teleportation of atoms should also be possible following a recent experiment at the Ecole Normale Supérieure in Paris that demonstrated that pairs of rubidium atoms could be entangled over distances of centimetres (see Hagley et al . in further reading).

As mentioned above, an important feature is that teleportation provides no information whatsoever
about the state being teleported. This means that any quantum state can be teleported. In fact, the quantum state does not have to be well defined; indeed, it could even be entangled with another photon. This means that a Bell-state measurement of two of the photons - one each from two pairs of entangled photons - results in the remaining two photons becoming entangled, even though they have never interacted with each other in the past (see right). Alternatively, one can interpret this "entanglement swapping" as the teleportation of a completely undefined quantum state (see Bose et al. in further reading). In a recent experiment in Innsbruck, we have shown that the other two photons from the two pairs are clearly entangled.

Quantum outlooks

We conclude by noting that, amazingly, the conceptual puzzles posed by quantum mechanics - and discussed for more than sixty years - have recently led to completely novel ideas that might even result in applications. These applications could include quantum communication, cryptography and computation. In return, these technological considerations lead to a better intuitive understanding of basic issues such as entanglement and the meaning of information on the quantum level. The whole field of quantum information technology is a classic example of basic physics and potential applications working hand in hand.

When an ultraviolet laser beam strikes a crystal of beta barium borate, a material with nonlinear optical properties, there is a small probability that one of the photons will spontaneously decay into a pair of photons with longer wavelengths (to conserve energy). The photons are emitted in two cones and propagate in directions symmetric to the direction of the original UV photon (to conserve momentum). In so-called type II parametric down-conversion, one of the photons is polarized horizontally and the other is polarized vertically. It is possible to arrange the experiment so that the cones overlap (see photograph). In this geometry the photons carry no individual polarizations ­ all we know is that the polarizations are different. This is an entangled state. (P G Kwiat et al. 1995 Phys. Rev. Lett. 75 4337)

Bob can send two bits of information to Alice with a single photon if they share a pair of entangled photons. To begin, one photon each is sent to Alice and Bob. The photons are in one of the four Bell states. Bob then performs either one of the three unitary transformations on his photon, transferring the pair into another Bell state, or simply does nothing ­ the fourth option. He then sends the photon to Alice who measures the state of the pair. Since there are four possible outcomes of this measurement, Bob has sent twice as much information as can be sent classically with a two-state particle.

When two particles are incident symmetrically on a 50/50 beam splitter it is possible for both to emerge in either the same beam (left) or in different beams (right). In general, bosons (e.g. photons) emerge in the same beam, while fermions (e.g. electrons) emerge in different beams. The situation is more complex for entangled states, however, and two photons in the Bell state |Y^­ñ emerge in different beams. Therefore, if detectors placed in the two outward directions register photons at the same time, the experimenter knows that they were in a |Y^­ñ state. Moreover, because we do not know the paths followed by the photons, they remained entangled.

Interference fringes can be observed in a two-path interferometer if there is no way of knowing, not even in principle, which path the particle takes. In a Mach­Zehnder interferometer a quantum particle strikes a beam splitter and has a 50/50 chance of being transmitted or reflected. Mirrors reflect both paths so that they meet at a second 50/50 beam splitter, and the numbers of particles transmitted/reflected by this beam splitter are counted. If no information about the path is available, the particle is in a superposition of the upper and lower paths. To observe interference one customarily varies the length of one of the paths (e.g. with a variable wave plate) and counts single clicks at the detectors as a function of this phase.

The scheme of Bennett et al. Alice wishes to teleport an unknown quantum state |Yñ (the "teleportee") to Bob. They agree to share an entangled pair of "ancillary" photons. Alice then performs a Bell-state measurement on the teleportee and her ancillary photon, and obtains one of the four possible Bell results. This measurement also projects Bob's ancillary photon into a well defined quantum state. Alice then transmits her result to Bob, who performs one of four unitary operations to obtain the original state.

n the experiment a pulse from a mode-locked Ti:sapphire laser (not shown) is frequency doubled, and the resulting UV pulse is used to create the entangled pair of "ancillary" photons in a nonlinear crystal. The UV pulse is then reflected back through the crystal to produce a second pair of photons: one is used as the teleportee while the other acts as a "trigger". Polarizers are used to prepare the teleportee photon in a well defined state, while various filters ensure that no path information is available about Alice's photons. Coincident photons detections at f1 and f2 project the photons onto a |Y^­ñ state (in which they have different polarizations). And since Alice's ancillary and Bob's photon are also entangled, this detection collapses Bob's photon into an identical replica of the original.

Author
Anton Zeilinger is in the Institut für Experimentalphysik, Universität Innsbruck, Technikerstrasse 25, A-6020 Innsbruck, Austria

 

Further reading

C H Bennett, G Brassard, C Crépeau, R Jozsa, A Peres and W K Wootters 1993 Teleporting an unknown quantum state via dual classic and Einstein­Podolsky­Rosen channels Phys. Rev. Lett. 70 1895­1899

C H Bennett and S J Wiesner 1992 Communication via one- and two-particle operators on Einstein­Podolsky­Rosen states Phys. Rev. Lett. 69 2881­84

D Boschi, S Branca, F De Martini, L Hardy and S Popescu 1998 Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein­Podolsky­Rosen channels Phys. Rev. Lett. 80 1121­1125

S Bose, V Vedral and P L Knight 1998 A multi-particle generalization of entanglement swapping Phys. Rev. A57 822­827

D Bouwmeester, J-W Pan, K Mattle, M Eibl, H Weinfurter and A Zeilinger 1997 Experimental quantum teleportation Nature 390 575­579

A K Ekert 1991 Quantum cryptography based on Bell's theorem Phys. Rev. Lett. 67 661­663

D M Greenberger, M A Horne, A Shimony and A Zeilinger 1990 Bell's theorem without inequalities Am. J. Phys. 58 1131­1143

D M Greenberger, M A Horne and A Zeilinger 1993 Multi-particle interferometry and the superposition principle Physics Today August pp22­29

E Hagley, X Maître, G Nogues, C Wunderlich, M Brune, J M Raimond and S Haroche 1997 Generation of EPR pairs of atoms Phys. Rev. Lett. 79 1­5

R Landauer 1991 Information is physical Physics Today May pp23­29

K Mattle, H Weinfurter, P G Kwiat and A Zeilinger 1996 Dense coding in experimental quantum communication Phys. Rev. Lett. 76 4656­4659